Tracking Mouse Movement, Part 2

In the previous post we discussed having shapes track the position of the mouse by rotating them to point towards the postion of the mouse on the canvas. It definitely works but for some shapes we want different behavior than simply rotating around the center of the shape.

For lines (or our turret!) we definitely want the behavior to be like the second line in the image rather than the first. To get this behavior we need to modify the coordinates of the line rather than just rotating it. If we think about a stationary line on our canvas with our mouse it probably looks something like this:

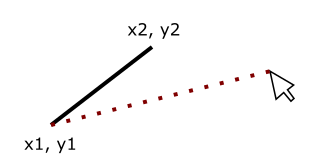
We’d like the line to be angled in the same way as the dotted red line so that it looks like this:

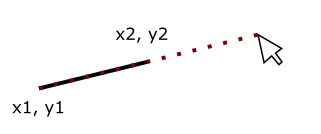
And we could make our line look like that if we knew what values of x2 and y2 that we needed in order to have our line point towards the mouse. This looks really familar though and we had a similar situation in the previous post trying to determine the angle we needed to rotate our shapes:

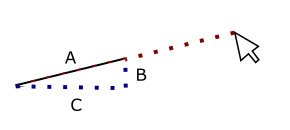
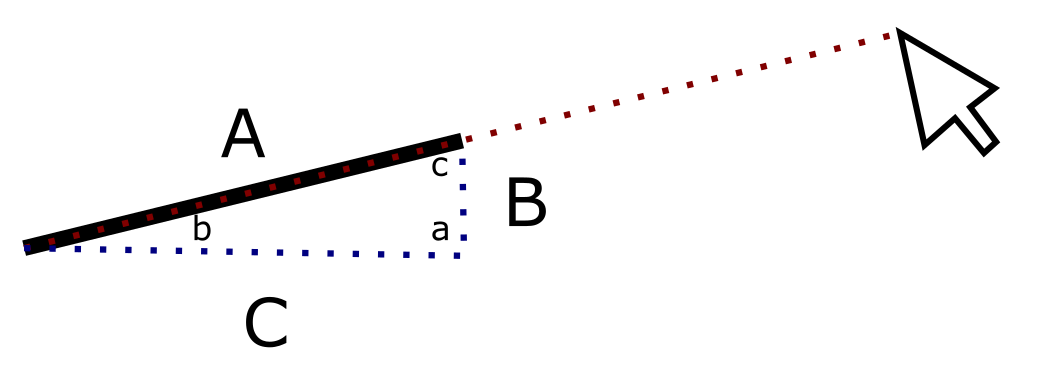
We know what A is…it’s just the length of our line. We don’t know what B and C are but if we did this would be easy, as we could just set x2 and y2 on our line based on those values:

line.x2 = line.x1 + C
line.y2 = line.y1 + B

So how do we get B and C? If we knew the angle we could use the Law of Sines to find the length of those sides. We know how to find that angle from the previous post but we had to use B to find it and we don’t know what B is in this case. Well, what do we know? If we ignore our line for a second we have a triangle that we can calculate the sides of:

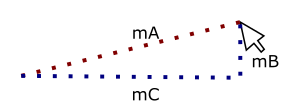
This is pretty much identical to what we did in the previous post. So how does this help us? The angles of this triangle are identical to the angles of the triangle that we made using our line. The only difference between the two trianlges are the lengths of the three sides. We can use the triangle formed by the mouse position and the x1 and y1 postion of our line to found our angle, then use the length of our line and the value of the angle to find B and C. Let’s walk through it.

First, we can find the angle $b$ using the law of sines like before:

$b = \sin(mB/mA)$

Now, let’s use the law of sines again to find B in our original triangle. Remember that $\sin(90) = 1$ and A is the length of our line:

$ B/\sin(b) = A/\sin(a)
B/\sin(b) = A
B = A/\sin(b) $

Now that we have B we can also calculate C the same way:

$C = A/\sin(c)$

What is $c$ though? We can calculate that. The angles of a triangle always add up to 180. $a = 90$ so $c = 90 - b$. With that our formula for C becomes

$C = A/\sin(90 - b)$

If we put this all together in code we would have something like this:

(This code and material is meant to be used with CMU Academy)

import math

barrel = Line(200, 200, 180, 200, fill="gray", lineWidth=5)

def onMouseMove(mouseX, mouseY):
   # Calculate the sides of the triangle
    C = abs(mouseX - barrel.x1)
    B = abs(mouseY - barrel.y1)
    A = math.sqrt(C**2 + B**2)

    if B != 0:
        b = math.asin(B/A)
    else:
        b = 0
    
    # A is always the length of our line. In this case it is 20
    A = 20
    
    
    # Now we can calculate B and C
    B = A * math.sin(b)
    # To do 90 - b we first have to convert our
    # angle to degress as python normally uses
    # radians
    b = math.degrees(b)
    
    # Calculate the angle c that we need
    c = 90 - b
    # And convert it to radians so we can use it
    c = math.radians(c)
    # Now we can calculate C
    C = A * math.sin(c)
    # We could also do all of the previous in one
    # line if we wanted:
    # C = A * math.sin(math.radians(90 - math.degrees(B)))
    
    # Adjust the width and height based on the quadrant 
    # of the x2 and y2 values
    if mouseX < barrel.x1:
        C = -C
        
    if mouseY < barrel.y1:
        B = -B

    barrel.x2 = barrel.x1 + C
    barrel.y2 = barrel.y1 + B

You’ll notice that we are once again adjusting values based on where the mouse is relative to the location of our line. If you remember back to the previous post that is because the calculations for our triangle assume we are always in quadrant 1. We have to adjust the values of B and C depending on what quadrant the mouse is in so that things behave as we expect.

With this we have one left thing to do…get shapes to chase after our mouse! Turns out that we already have everything we need in order to do that, but we’ll talk about the specifics in the next post.