Tracking Mouse Movement

In some cases we want to have an object track the position of the mouse. This may mean rotating something to face towards the mouse or knowing the direction the mouse is from something so that it can move towards it. In either case the calculations we have to perform are pretty much the same. If we have a shape and the mouse on the screen, where our shape is the group turret (imagine we are making a tank game)

base = Circle(200, 200, 10, fill="red")
barrel = Line(200, 200, 200, 180, fill="red", lineWidth=5)
turret = Group(base, barrel)

we can imagine a triangle connecting the center of the shape to the tip of the mouse

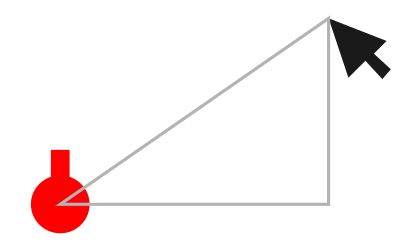
If we remove the shape and the mouse for a moment we are left with a triangle with three sides and three angles.

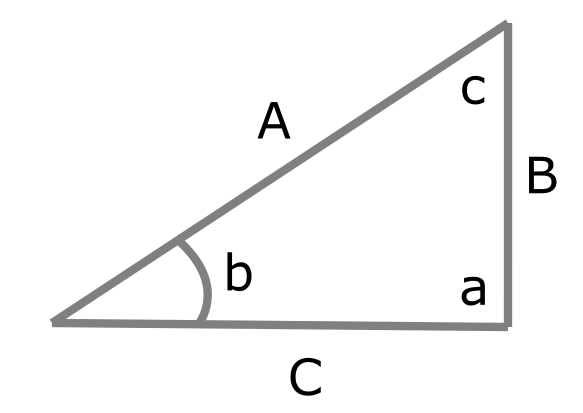
What do we know about this triangle? Well, right away we can easily find out the length of all three sides: A, B, and C. If mouseX and mouseY are the coordinates of the mouse and x and y are the coordinates of the center of the shape, then we know that

C = mouseX - x
B = mouseY - y

and we can calculate A by using the pythagorean $a^2 = b^2 + c^2$

import math
A = math.sqrt(C**2 + B**2)

We also know the angle a is that is going to be 90 degrees in a right triangle. The leaves us with needing to find out the angle b. We can use the Law of Sines to figure this out. It states $A/\sin(a) = B/\sin(b) = C/\sin(c)$. Since we already know A, a, and B, we can solve

$A/\sin(a) = B/\sin(b)$

We can simplify this even more because a is 90 degrees and $\sin(90) = 1$, giving us

$ A = B/\sin(b)
\sin(b) = B/A
b = \arcsin(B/A) $

Putting this into Python code we get

import math

C = mouseX - x
B = mouseY - y
A = math.sqrt(C**2 + B**2)

if B != 0:
    b = math.asin(B/A)
    # We need to convert a to degrees since python defaults to returning radians
    b = math.degrees(a)
else:
    b = 0

Why do we have if B != 0? If the vertical distance between the mouse and the shape becomes 0 then the mouse is directly the right (in this example) of the shape, which means the angle is really just 0. If we didn’t include that we’d solve for A as $A = \sqrt{C^2 + 0^2}$ which would end up making $A = C$ and $\arcsin(C/C)$ is $\arcsin(1)$ which is 90 degrees. That calculation would result when either B == 0 or C == 0, but it’s only correct when C == 0 so we want to have a condition for when B == 0.

Once we have the angle a we can figure out how to rotate our shape…almost. One thing to note is that doing this calculation only gives us an angle between 0 and 90 degrees. In fact, if we were to sketch out the way the angle would be calculated depending on where the mouse was relative to our shape (with our shape being in the center of the diagram) it would look something like this:

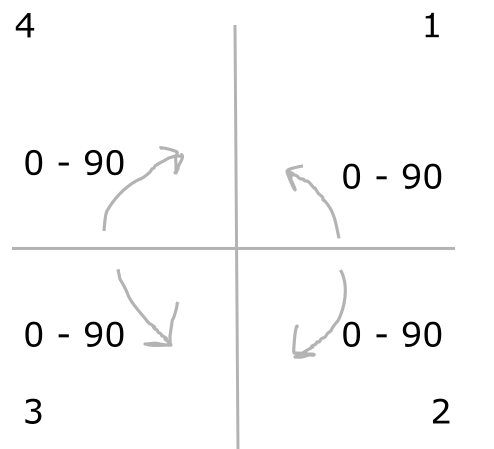
Immediately we notice that this doesn’t give us a nice angle that we can use to adjust our shape. We will have to do some additional math and adjust our angle based on what quadrant our mouse is in. In fact, not only do we have to adjust the angle for each quadrant, we also have to adjust the angle to take in to account that for shapes increasing the angle always rotates the shape clockwise and decreasing the angle rotates it counter-clockwise. This is backwards from how our angle is calculated in the first quadrant. Effectively we want have the angle we calculate start a 0 for the horizontal axis in quadrant 2 and increase going clockwise starting at quadrant 2. This would give us the following angles as the mouse made a clockwise circle around the shape starting in quadrant 2:

Mouse Quadrant	Angles in Quadrant
2	0 - 90
3	90 - 180
4	180 - 270
1	270 - 360

I’ve labeled them 1 through 4 in the diagram and we can use the mouse and shape coordinates to adjust our calculated angle:

if mouseX > x and mouseY > y: # This is quadrant 2
   # Do nothing...we could just leave this IF statement out entirely
   pass
elif mouseX < x and mouseY > y: # This is quadrant 3
   # We want the angle to start at 90 and continue through to
   # 180. We can get this by subtracting our calculated angle
   # from 180, as the calculated angle starts at 90 and decreases as we move
   # clockwise.
   b = 180 - b
elif mouseX < x and mouseY < y: # This is quadrant 4
   # This quadrant is more straightforward. It goes from 180 to 270, and
   # our calculated angle starts at 0 and goes to 90.
   b = 180 + b
elif mouse > x and mouseY < y: # This is quadrant 1
   # This is pretty much the same thing as quadrant 3, but
   # instead of ending at 180 we end at 360.
   b = 360 - b

Once this calculation is done the resulting angle stored in a should smoothly go from 0 to 360 as we move the mouse clockwise around the quadrants, starting in quadrant 2. We now have a value we can use to rotate our shape by settings the shape’s rotateAngle property to a. If we do this we will still notice that our shape doesn’t quite follow the mouse as we expect, but is instead a bit behind. This is because the rotateAngle property is relative to the starting position of our shape. Since our shape was originaly pointing up, that orientation represents a rotation angle of 0. Our calculations though consider 0 to be a starting position pointing left. To fix this we can either change the starting position of our shape or add an offset to our rotation angle to compensate. Since we are 90 degrees off, we could simple set rotateAngle = a + 90 and things should work as expected.

If you look closely the rotation of our shape doesn’t quite look right. It isn’t really rotating around the center of the circle but some other spot. This is due to how the Group calculates the center. Is based on the positon of the circle and the line shape together, so it isn’t really where we’d want it to be. We could try to move the line shape to point towards the mouse by adjusting its rotation, but that would rotate it around the center of the line when we really want the end of the line that is in the middle of the circle to stay where it is and the other end of the line to point towards the mouse. We’ll explore how to do that in the next post.

Full Code

(This code and material is meant to be used with CMU Academy)

import math

base = Circle(200, 200, 10, fill="red")
barrel = Line(200, 200, 200, 180, fill="red", lineWidth=5)
turret = Group(base, barrel)

def calculate_angle(x, y, mouseX, mouseY):
    # Calculate the sides of the triangle
    C = abs(mouseX - x)
    B = abs(mouseY - y)
    A = math.sqrt(C**2 + B**2)
   
    if B != 0:
        b = math.asin(B/A)
        # We need to convert a to degrees since python defaults to returning radians
        b = math.degrees(a)
    else:
        b = 0

     # Adjust the angle based on quadrant
    if mouseX > x and mouseY > y: # This is quadrant 2
       pass
       # Do nothing...we could just leave this IF statement out entirely
    elif mouseX < x and mouseY > y: # This is quadrant 3
       # We want the angle to start at 90 and continue through to
       # 180. We can get this by subtracting our calculated angle
       # from 180, as the calculated angle starts at 90 and decreases as we move
       # clockwise.
       b = 180 - b
    elif mouseX < x and mouseY < y: # This is quadrant 4
       # This quadrant is more straightforward. It goes from 180 to 270, and
       # our calculated angle starts at 0 and goes to 90.
       b = 180 + b
    elif mouseX > x and mouseY < y: # This is quadrant 1
       # This is pretty much the same thing as quadrant 3, but
       # instead of ending at 180 we end at 360.
       b = 360 - b

    return b
    
def onMouseMove(mouseX, mouseY):
    # Get the angle
    a = calculate_angle(turret.centerX, turret.centerY, mouseX, mouseY)
    # Rotate the turret based on the angle, plus an offset of 90 degrees
    # to adjust based on the starting position of the turret
    turret.rotateAngle = a + 90
    
    # If we uncomment this and comment out the above line we will
    # rotate just the barrel...but that isn't right either!
    # barrel.rotateAngle = a + 90